1. 标题
基于自适应近邻传播算法探索多维时空点模式
Exploring Multidimensional Spatiotemporal Point Patterns Based on an Improved Affinity Propagation Algorithm
2. 成果信息
Cui H, Wu L, He Z, et al. Exploring Multidimensional Spatiotemporal Point Patterns Based on an Improved Affinity Propagation Algorithm[J]. Int. J. Environ. Res. Public Health, 2019, 16(11), 1988.
https://doi.org/10.3390/ijerph16111988
This study was financially supported by the National Natural Science Foundation of China (41871311), the National Key Research and Development Program (Grant No: 2017YFB0503600), the Teaching Innovation Funds of Central Universities (2019G56).
3. 成果团队成员
崔海福(第一作者),博士生,中国地质大学地理与信息工程学院。研究方向:时空数据挖掘与知识发现。
吴亮(通讯作者),教授,中国地质大学地理与信息工程学院。研究方向:空间分析建模和应用,空间信息服务。
何占军,助理研究员,中国地质大学地理与信息工程学院。研究方向:时空数据统计分析与关联模式挖掘。
胡胜,博士生,中国地质大学地理与信息工程学院。研究方向:空间分析建模和应用。
马凯,博士,中国地质大学地理与信息工程学院。研究方向:地质大数据挖掘。
尹力,Associate Professor,University at Buffalo, The State University of New York · Department of Urban and Regional Planning,研究方向:Quantitative Social Research, Geostatistics and Geoinformatics (GIS)
陶留锋,博士,中国地质大学地理与信息工程学院。研究方向:空间分析与信息服务。
4. 成果介绍
空间聚类是一种重要的数据分析技术,它通过搜索和识别出有限的类别集来描述空间数据。通过聚类,可以识别数据分布的密集和稀疏区域,进而确定数据之间的关系与全局分布模式。随着具有时间属性的空间数据不断涌现,时空聚类得到了发展。时空数据聚类可以在一系列具有时序特征的事件中获得空间分布规律,通过识别热点区域,生成新的空间研究单元。
国内外学者对时空数据聚类方法进行了多方面的研究,但对数据(如轨迹点)计算前必须设置初始聚类中心、聚类半径等敏感参数,而不同的参数设置会产生不同的结果。且以往的研究不能处理非欧氏空间中的数据聚类问题。此外,在对多维时空数据进行分析时,必须同时考虑位置特征、时间属性和主题属性,才能得到准确的结果。因此,提出一种在较少的参数设置情况下,能够处理多维属性的时空数据聚类方法---自适应的近邻传播聚类算法(MDST-AP)。
本文综合考虑时空数据不同尺度下的多维属性,应用高斯核变换解决线性不可分的问题。针对AP聚类算法的参数选择,提出一种自适应参数的设置方法,减少了人工定义参数的局限性。最后,利用北京出租车轨迹数据进行实验,验证MDST-AP算法的有效性。图1为MDST-AP算法流程图。

图1 MDST-AP算法流程图
(1) 多维属性的度量
传统的聚类方法在对空间实体进行聚类时只考虑特征属性或位置属性,而提出的MDST-AP方法可以同时计算空间属性、时间属性和主题属性之间的相似度。以出租车轨迹点数据为例,它包括纬度和经度、速度和方向属性(或更多属性),通过所有这些属性值之间的距离来考虑两点之间的相似度。
(2) 高斯核函数下的相似性计算
对于AP聚类的欧氏空间线性不可分问题,本文采用高斯核空间进行计算。核技术可以提供从线性到非线性特征的连接,并表示两个向量之间的点积。如果将输入数据映射到一个高维空间,那么在这个高维空间中的操作在原始空间中是非线性的。MDST-AP计算多维时空数据之间的相似度时,用标准核空间距离代替原算法的欧氏距离测度。
(3) 自适应步长的偏向参数(P)设置
在AP算法中,偏向参数P被设置为相似度的均值或中值,这样可以得到确定的聚类,但不一定是最佳的聚类。根据AP算法的原理,当每个数据点的相似度相同时,聚类数随P值的增加而增加。也就是说,不同的P值有不同的聚类评价结果。因此,在P最大值与最小值之间以等距离方式进行取值实验,直到取得最佳的聚类数。本文选取Davies-Bouldin(DB)指标对聚类结果进行评价,并根据评价结果确定最终的P值。
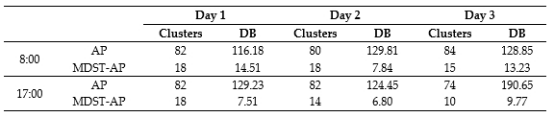
本研究中随机选择三个工作日早、晚高峰轨迹点数据进行实验,对比AP和MDST-AP算法的聚类结果。根据表1可知,AP聚类结果中的类别数目和DB值是MDST-AP算法的约10倍和5倍。在分析大规模的时空数据时,如果聚类数目过大,不利于拥塞检测,人工判断的工作量会增加,导致相当大的数据冗余。通过GPS数据聚类实验,验证了MDST-AP算法的有效性。
表1 算法对比结果
此外,我们使用点匹配准确率(ARP)来量化MDST-AP算法的准确度。图2显示,在1000米缓冲区内,k-means算法、AP算法和MDST-AP算法的平均ARP分别达到72.51%、75.18%和81.47%。一般来说,在进行时空数据聚类时,MDST-AP算法要比k-means算法和AP算法更可靠。

图2 MDST-AP算法流程图
创新点:
Ø 采用高斯核空间代替欧几里德空间来度量空间属性和非空间属性的相似性,解决了聚类多维数据时线性不可分问题;
Ø 利用自适应步长的方法设置相似度,减少了算法的迭代次数,更快地取得最佳的聚类结果。