1. 标题

· 基于遗传算法优化的极限学习机浅海水深反演

· Detecting Water Depth from Remotely Sensed Imagery Based on ELM and GA-ELM

2. 成果信息

· Guizhou Zheng, Weihua Hua, Zhonghang Qiu, Zimei Gong. (2021). Detecting Water Depth from Remotely Sensed Imagery Based on ELM and GA-ELM. Journal of the Indian Society of Remote Sensing. 49(4):947–957. Doi:https://doi.org/10.1007/s12524-020-01270-w

3. 团队成员

· 郑贵洲(第一作者，通讯作者)，博士，中国地质大学（武汉）地理与信息工程学院，教授。主要从事资源与环境遥感、三维地理信息系统及深度学习与大数据研究。E⁃mail：zhenggz@cug.edu.cn。

· 花卫华，博士，中国地质大学（武汉）地理与信息工程学院，教授。主要从事基于计算几何与机器学习的三维地质建模，大规模三维地质模型的存储、网络传输与高性能三维可视化，三维地质模拟与可视化技术在城市地质与地下空间中的应用等。

· 邱中航，硕士研究生，武汉大学资源与环境科学学院。研究方向为遥感图像处理、图像超分辨率。

· 龚子美，硕士研究生，中国地质大学（武汉）地理与信息工程学院。研究方向为地理数据挖掘与空间大数据分析。

4. 成果介绍

一、研究内容：

遥感浅海水深反演是水深测量的重要技术和方法，对海洋工程、航运及海洋军事安全等具有重要意义。本研究以南海太平岛附近海域为例，通过遗传算法对超限学习机（ELM）的输入层权值和隐含层阈值进行调整，构建基于遗传算法优化的超限学习机（GA-ELM）水深反演模型。选取WorldView-2高分辨率遥感影像的8个多光谱波段作为输入层，S57海图资料中获取的水深数据作为输出层，sigmoid函数作为模型的激活函数，反演得到实验区12m以内的浅海的水深。最后对反演水深和实测水深进行非线性回归分析，利用平均相对误差（Mean Relatively Error, MRE）、均方根误差（Root Mean Square Error, RMSE）和平均绝对误差（Mean Absolute Error，MAE）等进行精度评价。

二、研究方法

遗传算法具有良好的全局搜索能力，可扩展性良好，易于与其他算法相结合，本文采用遗传算法优化的极限学习机算法，通过调整和优化输入权值矩阵和隐含层偏差，提高极限学习机网络的精度。首先利用遗传算法全局搜索特性，优化极限学习机的输入权值和隐含层偏差，使得网络输出能够满足误差要求，若未满足，调整输入权值和隐含层偏差等参数并重新进行训练。与传统的需要优化输入权重、隐含层偏差和输出权重的神经网络相比，遗传算法只需要对输入权重和隐含层进行优化，从而减少了计算量，研究的具体流程如图1所示：

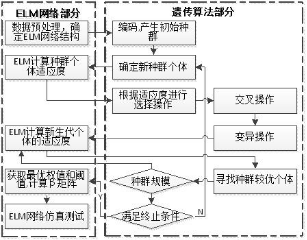
图1 基于遗传算法优化的超限学习机训练流程

（1）确定极限学习机网络的拓扑结构，选择并确定输入神经元个数、隐含层神经元个数和输出层神经元个数。读取样本数据，将样本数据分为训练集和测试集，并将数据进行归一化处理。

（2）随机产生一组极限学习机网络的输入权值和隐含层偏差，对其进行编码并生成初始种群。设定遗传代数、个体长度、代沟、交叉和变异概率。

（3）解码得到输入权值和隐含层偏差，并赋值给极限学习机网络。使用训练集训练网络，利用训练好的网络进行网络测试，为了使预测值和期望值的残差尽可能小，将测试样本的期望值和预测值的均方根误差作为适应度函数。

（4）对种群进行选择、交叉和变异操作，得到新的种群，检验其是否满足终止条件。如果满足条件，则得出优化后的极限学习机输入权值和隐含层偏差；若不满足条件，则返回步骤（2）。

（5）将优化后的权值和阈值进行极限学习机网络训练，计算隐含层输出矩阵H，并求解矩阵H的Moore-Penrose广义逆矩阵 。计算输出层权值 ，最终将测试集带入到训练好的网络模型中进行测试。

三、实验结果： 

研究使用70组验证集进行精度检验，为了定量地对比分析两个水深反演模型的拟合效果和反演精度，利用平均相对误差（MRE）、均方根误差（RMSE）和平均绝对误差（MAE）三个指标对网络模型精度进行评价。

在之前的研究中，作者曾使用相同数据对实验区海域进行基于二阶多项式回归和神经网络方法的浅海水深反演实验，我们将其结果与ELM、GA-ELM网络模型的精度指标进行比较，评价结果如表1所示。

表1 不同水深反演模型的精度指标对比

从表中可以看出，ELM和GA-ELM模型反演的水深值与实测水深值的平均相对误差较小，均方根误差均在0.8以下，而平均绝对误差也均在0.8以下，说明两种反演模型反演的水深值均具有较高的精度，整体误差较小，反演结果可靠。同时，GA-ELM反演模型的三项参数相比较ELM都要更好，说明经遗传算法优化后的ELM网络模型的精度高于普通的ELM网络模型。

通过与其他三种水深反演模型对比可以发现：GA-ELM模型比二阶多项式回归模型的水深反演效果更好，R²由二阶多项式回归模型的0.8813提高到0.9509，但相比BP神经网络的R²值 0.9556和RBF神经网络的R²值0.9959稍低。同时通过对比其他精度评价指标，可知GA-ELM模型 的RMSE值0.6288相比较BP神经网络模型的RMSE值1.8321和RBF神经网络模型的RMSE值0.8922有所减少，表示GA-ELM比BP神经网络模型和RBF神经网络模型具有更好的稳定性。

根据精度分析结果，利用建立好的ELM网络模型和GA-ELM网络模型对研究区海域进行水深反演，结果分别如图2、3所示。

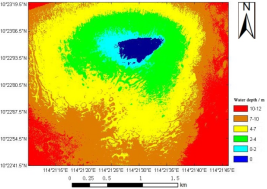
图2 基于ELM模型的研究区水深反演图  图3 基于GA-ELM模型的研究区水深反演图

从图中可以看出：水深反演的实验区域最大水深值为12m左右，两个模型的水深反演图海陆分界清晰，水深值均由岛屿向海水方向呈逐渐增加趋势。通过与S57海图数据对比，可知两个模型的整体水深反演结果与实验区域的实际情况一致，反演结果可靠。

由于可见光在水体中随着海水深度的增加而不断衰减，从而导致反演结果随着深度的增加而变差。根据图2、3可以看出在0-7m水深区域ELM和GA-ELM两个反演模型的反演结果基本一致，显示水深反演结果较好。而在7-12m水深区域处，两个模型的反演结果虽然基本一致，但 ELM的水深反演结果图在两个相邻水深深度层之间出现了边缘破碎的情况，GA-ELM水深反演的结果相较ELM要稍好一点，边缘破碎现象不太明显，这可能与光在水体中的衰减有关：随着水体深度的增加，两个水深反演模型由于精度原因在水深反演结果的细节上会出现不同。

四、结论：

本文以南海南沙群岛北部的太平岛及其附近海域为研究区域，利用高分辨率卫星WorldView-2和S57海图数据，针对现有非线性水深反演模型网络参数复杂和泛化能力不强的缺点引入超限学习机及遗传算法对其的改进算法，构建ELM水深反演模型和遗传算法优化的ELM水深反演模型，并对两个模型进行比较分析，得出以下结论：

（1）高分辨率多光谱卫星WorldView-2在中国南海南沙群岛海水域水深遥感反演中能够获得很高的精度，为研究南海岛礁浅海水深、海域环境监测、海域军事安全等提供了更加有效的数据支持。

（2）ELM水深反演模型能够在实验区取得很好的反演结果，各项精度指标均较高，而经过遗传算法优化后的模型与原模型相比精度有较大提高，平均相对误差由22.05%减少到11.51%，平均绝对误差由0.7043减少到0.5111，均方根误差由0.7734减少到0.6288，表明本文提出的基于遗传算法优化的超限学习机水深反演方法具有实际应用价值。

（3）遗传算法优化的ELM网络模型相比普通的ELM网络模型结构更紧凑，但由于ELM的输入权值矩阵和隐含层偏差需要经过遗传算法优化，受迭代次数影响，训练时间会更长。

（4）因为GA-ELM模型具有非线性特性，与传统的单波段和多波段水深反演方法相比，遗传算法优化的ELM水深反演模型具有更好的泛化能力和反演精度。与bp神经网络和RBF神经网络模型相比，GA-ELM模型虽然在反演精度上略差，但反演结果更具有稳定性。

（5）卫星影像由于其生产过程的特殊性，相比传统方法更容易受到如大气、潮汐、水体环境、波浪等环境因素的影响。由于各种原因，本次研究未考虑这些因素的影响。未来会将重点研究如何解决这些因素对于水深反演的影响，进一步提高遥感水深反映的精度和可靠性。